Phragmén–Lindelöfの定理の証明

あけましておめでとうございます。
厄年を発熱で迎え、最悪の三が日を過ごしました。
お祓いいこうかなぁ・・・

さて、今回は久しぶりに純粋な数学の記事でございます。
数学界には多額の懸賞がかかったミレニアム問題が存在するのは有名な話ですが、今日はその内の一つである、Riemann予想に関連したものです。

あまり余計なこと書かず、自分用のメモ程度に書きますので、この定理の関連等が気になる人は自分で調べてください。

Phragmén–Lindelöfの定理の証明

ここでは証明を省きますが次の定理1を認めて話を進めます。

定理1

$f(s) \,\, (s = \sigma + it)$ は領域 $\delta: \alpha \leq \sigma \leq \beta, t \geq 0$ で正則とし、 $\delta$ の境界上で $|f(s)| \leq M$ とする。このとき $\delta$ 内で

$\left|f(s)\right| \leq Kt^\gamma , \gamma > 0$

なる定数 $K, \gamma$ が存在すれば、 $\delta$ 内でも

$\left|f(s) \right| \leq M$

である。

Phragmén–Lindelöfの定理

$f(s) \,\, (s = \sigma + it)$ は領域 $\delta: \alpha \leq \sigma \leq \beta, t \geq 0$ で正則とし、 $\delta$ 内で

$\left|f(s) \right| \leq Kt^\gamma , \gamma > 0$

なる定数 $K, \gamma$ が存在するとする。このとき $t \to \infty$ で

$\left|f(\alpha + it) \right| = O(t^a), \,\, \left|f(\beta + it) \right| = O(t^b)$

ならば、

$\left|f(\sigma + it) \right| = O( t^{ a\frac{\beta-\sigma}{\beta-\alpha} + b\frac{\sigma-\alpha}{\beta-\alpha} } )$

である。

証明

$s = \rho e^{i \phi}$ とする。このとき $\log{s} = \log{\rho} + i \phi$ とすれば、 $\log{s}$ は一意的に定まる。
ここで、

$\phi(s) = a\frac{\beta-s}{\beta-\alpha} + b\frac{s-\alpha}{\beta-\alpha}, \,\,\, \phi(\sigma) = a\frac{\beta-\sigma}{\beta-\alpha} + b\frac{\sigma-\alpha}{\beta-\alpha}$

とおけば、

$\phi(s) = \phi(\sigma) + \frac{b - a}{\beta-\alpha}ti$

が成立する。

ここで新たに

$g(s) = e^{ \phi(s) \left( \log{s} - \frac{\pi}{2}i \right) }$

とする。このとき $s = \sigma + it \,\, (\alpha \leq \sigma \leq \beta, t > 0)$ に対して、

$\displaystyle \begin{eqnarray} \left| \log{s} - \log{t} - \frac{\pi}{2}i \right| &=& \left| \log(s) - \log{ti} \right| \\ &=& \left| \int_{\sigma + ti}^{ti} \frac{du}{u} \right| \leq \int_{\sigma + ti}^{ti} \frac{|du|}{|u|} \leq \frac{|\sigma|}{t} \\ &\leq& \frac{ {\rm Max} ( |\alpha| , | \beta| ) }{t} \leq \frac{K}{t}\,\,\,\,\,\, (K = {\rm const.} ) \end{eqnarray}$

となる。よって

$\displaystyle \log{s} - \frac{\pi}{2}i = \log{t} + O \left(\frac{1}{t} \right)$

が得られる。以上より、 $K_1, K_2, K_3, \dots$ を定数として、

$\displaystyle \begin{eqnarray} g(s) &=& e^{ \phi(s) \left( \log{s} - \frac{\pi}{2}i \right) } \\ &=& e^{ \phi(\sigma)\log{t} + i\frac{b-a}{\beta - \alpha}t\log{t} + \theta_1 } \,\,\,\, ( |\theta_1| \leq K_1)\\ \end{eqnarray}$

となり、

$\displaystyle |g(s)| \leq K_2 t^{\phi(\sigma)} , \,\, \left|\frac{1}{g(s)} \right| \leq K_3 t^{-\phi(\sigma)}$

が成立する。

ここで $F(s) = f(s)/g(s)$ とおくと、

$\displaystyle |F(s)| = \left| \frac{f(s)}{g(s)} \right| \leq K_4 t^{\gamma - \phi(\sigma)} = K_4 t^{\gamma'}$

なので $F(s)$ は定理1の条件を満足する。よって領域 $\delta$ 内で有界。つまり左右それぞれの境界上では $t \to \infty$ で

$\displaystyle \begin{eqnarray} F(s) &=& O(t^a)O(t^{-a}) = O(1) \\ F(s) &=& O(t^b)O(t^{-b}) = O(1) \end{eqnarray}$

よって、

$\displaystyle |f(s)| = |f(\sigma + it)| = | g(\sigma + it) F(s) | = |g(\sigma + it) O(1)| = O(t^{\phi(\sigma)})$

となる。(証明終了)

これとゼータの関係

リーマン予想は $\sigma = 1/2$ の値に興味があるわけですが、 f:id:ket-30:20170106183921j:plain:w300:h300
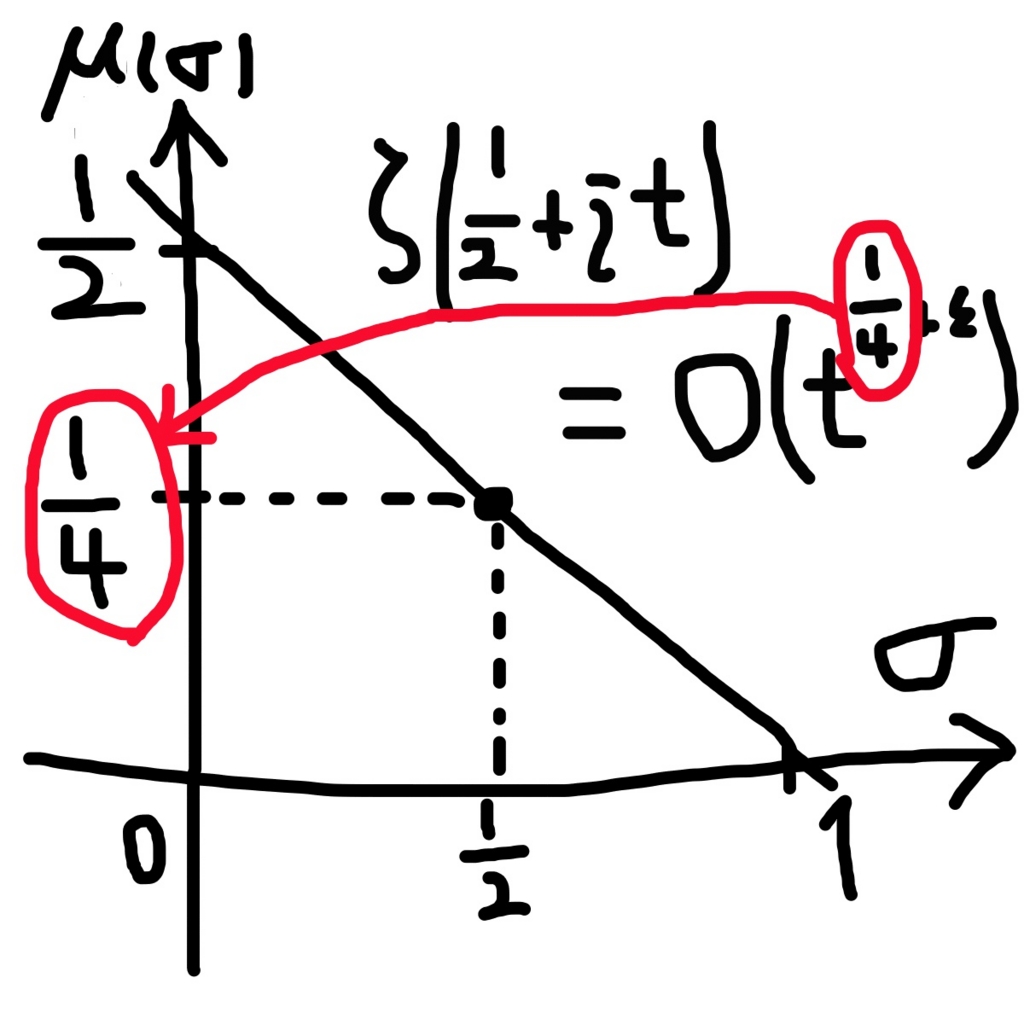
こうなりました。縦軸は $\sigma$ のときにゼータがとる値の指数部分を表しています。直線がちょっと上にずれてるのは $\varepsilon$ を表現したつもりです。(ずれただけ)