崩壊型ギブスサンプリングを用いたトピックモデルの実装

こんにちは．

GWですね．最高の実装日和です．

トピックモデル (機械学習プロフェッショナルシリーズ)

今回は上の本を読み，p77の実験を追試したので簡単にまとめます．

学習の際には持橋先生のスライドがとても参考になりました．

余談ですがこの本は数式展開がとても丁寧です．ディリクレ分布に慣れてしまえば数式レベル自体も高くなく，とても読みやすいです． 疑似コードも書いてあり実装する際にとても役立ちます．

この記事では理論に関して詳しい説明しませんので，気になっている方がいたら是非購入することをお勧めします．

さてダイレクトマーケティングが済んだので本題に行きましょう．

トピックモデル (Topic Model)

まずは，簡単にトピックモデルの解説をしていきます．

トピックモデルとは文書データの解析手法として提案されたもので，大量の文書データから注目されているトピックを抽出することができます．

またトピックモデルを用いると，文書を構成する単語にトピックを付与することができます．文書そのものではなく単語にトピックを付与することで，ひとつの文書に複数のトピックを与えることが可能になり，より厳密な分析をすることができます．

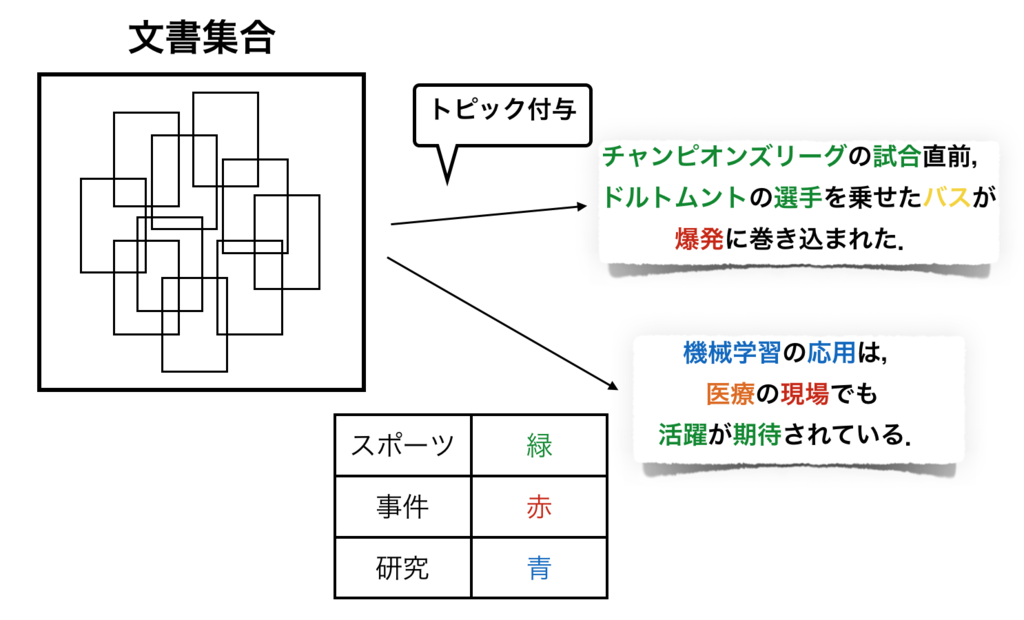
上の図はそれぞれの単語にトピックを付与するイメージ図です．
単語の色は，その単語がどのトピックに属しているのかを表しています．図の中では緑，青，赤の三色しかトピックの定義づけをしていませんが，黄色やオレンジも何らかのトピックに属していると考えてください．

一例として1つ目の文書は，最近起こった事件に基づいて僕が適当に作った文書です．
この文書をトピックモデルによって分析した場合，サッカーに関係する単語が多くスポーツのトピックを持っている反面，爆発という単語から事件性を孕んだ文書であるということがわかります．

崩壊型ギブスサンプリング

崩壊型ギブスサンプリングは，トピックモデルを学習させる手法の1つです． 今回の実装もこの手法を使っています．

先に文字の定義をしておきましょう．

---

: 文書数

: トピック数

: 文書に含まれる単語数 (文書長)

: 全文書で現れる単語の種類数 (語彙数)

: 文書集合

: 文書

: 文書の番目の単語

: 文書集合全体でトピックが割り振られた単語数

: 文書でトピックが割り振られた単語数

: 文書集合全体で語彙にトピックが割り振られた単語数

: 文書でトピックが割り当てられる確率

: トピックのとき，語彙が生成される確率

: 文書の番目の単語に付与されたトピック

: トピック集合

---

この手法の勘所はパラメータの積分消去です． トピック分布集合と単語分布集合を次のように周辺化することができます．

ここでは事前分布のパラメータを表しています．一様ディリクレ分布を仮定しているので，ベクトルではなくスカラーです．

このようにパラメータを積分消去することで推定するパラメータの数を減らし，より効率的な推定が可能になります．

またギブスサンプリングをするには，サンプリング式が必要です．

文書の番目の単語がトピックに分類される確率は，そのトピックを除いたトピック集合と文書集合が与えられたときの条件付き確率

で与えられます．

それぞれの項は式の右辺から，ディリクレ分布を用いて計算できます．結果的にサンプリング式は次のように求められます．

ハイパーパラメータは不動点反復法で推定することができ，更新式は以下のようになります．ちなみにはディガンマ関数です．

これらの式を用いて，

1. 単語ごとにサンプリング確率を計算し，トピックを付与．
2. 全ての単語にトピックが振られたら，ハイパーパラメータの更新．

の手順を収束するまで繰り返すことでトピックを自動で抽出していきます．

実装&実験

実験は青本のp77に書いてある方法とほぼ同じ条件で行いました． 言語はpythonです．

1. 日本語wikipediaから10万文書抽出する．
2. その中から頻出単語5000語彙を抽出し語彙集合とする.
3. ランダムに1万文書を選択し，語彙集合に基づいたBOWを作成する．
4. トピックモデルを用いて，トピックを抽出する．

手順はざっとこんな感じです． 青本ではトピック数を50にして実験した結果が載っていますが，手元の実験ではトピック数を20にして実験しました．

実行時間は一単語ずつ見ているせいか，100epochで12時間程度かかりました．なかなか時間かかってます．多分何も工夫せず実装しているせいもあると思うので，何かしらアドバイスがある方はぜひコメントください．よろしくお願いします．

以下実装したコードの一部です．
全コードはgitに上げているのでそちらを参照願います．

github.com

class TopicModel():

    def __init__(self, BOWs, K=20, V=5000, max_words=2000, ratio=0.9 ,alpha=1.0, beta=1.0):
        self.BOWs = BOWs
        border = int(ratio * self.BOWs.shape[0])

        self.train_BOWs, self.test_BOWs = np.vsplit(self.BOWs, [border])

        self.V = V
        self.K = K

        self.alpha = alpha
        self.beta  = beta

        self.D = self.train_BOWs.shape[0] 
        self.test_D = self.test_BOWs.shape[0]

        self.N_dk = np.zeros([self.D, self.K]) 
        self.N_kv = np.zeros([self.K, self.V]) 
        self.N_k  = np.zeros([self.K, 1]) 

        self.z_dn = np.zeros([self.D, max_words]) - 1 

    def fit(self, epoch=100):

        self.pplx_ls = np.zeros([epoch])

        for e in range(epoch):
            print("Epoch: {}".format(e+1))

            for d, BOW in enumerate(self.train_BOWs):
                sys.stdout.write("\r%d / %d" % (d+1, self.train_BOWs.shape[0]))
                sys.stdout.flush()

                for n, v in enumerate(BOW):
                    if v < 0: break

                    current_topic = int(self.z_dn[d, n])

                    # reset information of d-th BOW
                    if current_topic >= 0:
                        self.N_dk[d, current_topic] -= 1
                        self.N_kv[current_topic, v] -= 1
                        self.N_k[current_topic] -= 1

                    # sampling
                    p_z_dn = self._calc_probability(d, v)
                    new_topic = self._sampling_topic(p_z_dn)
                    self.z_dn[d, n] = new_topic

                    # update counting
                    self.N_dk[d, new_topic] += 1
                    self.N_kv[new_topic, v] += 1
                    self.N_k[new_topic] += 1


            # update α
            numerator = np.sum(digamma(self.N_dk+self.alpha))\
                      - self.D*self.K*digamma(self.alpha)
            denominator = self.K*(np.sum(digamma(np.count_nonzero(self.train_BOWs+1,axis=1)+self.alpha*self.K))\
                        - self.D*digamma(self.alpha*self.K))
            self.alpha *= numerator / denominator

            # update β
            numerator = np.sum(digamma(self.N_kv+self.beta)) - self.K*self.V*digamma(self.beta)
            denominator = self.V*(np.sum(digamma(self.N_k+self.beta*self.V)) - self.K*digamma(self.beta*self.V))
            self.beta *= numerator / denominator

実験結果

最終的に抽出されたトピック例をpandasを使って眺めてみましょう．そのトピックに割り当てられた数が多い順に単語が並んでいます．

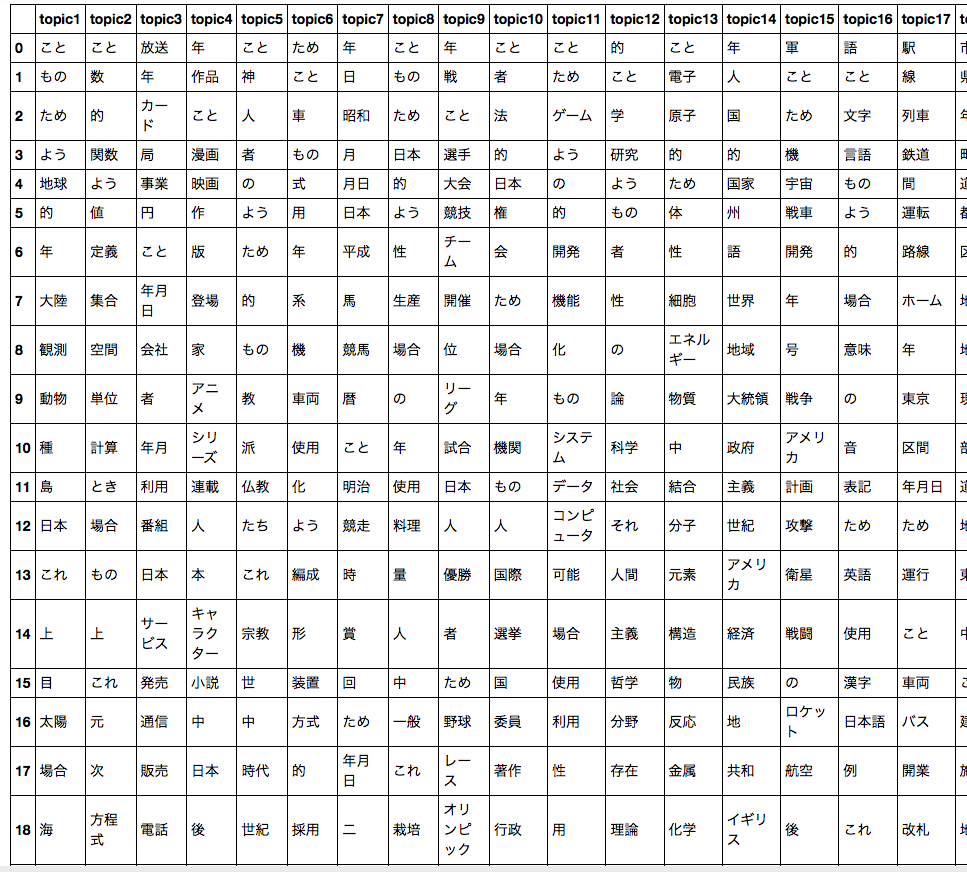
目がチカチカする・・・．

１個ずつ確認してみましょう．

まずはトピック2．

'こと', '数', '的', '関数', 'よう', '値', '定義', 
'集合', '空間', '単位', '計算', 'とき', '場合', 
'もの', '上', 'これ', '元', '次', '方程式', '点'

完全に数学ですね．うまいこと数学というトピックが抽出できています．

もうひとつ，トピック9．

'年', '戦', 'こと', '選手', '大会', '競技', 'チーム', 
'開催', '位', 'リーグ', '試合',  '日本', '人', '優勝', 
'者', 'ため', '野球', 'レース', 'オリンピック', 'プロ'

これは野球トピックが抽出できていますね．いい感じです．

トピックモデルを用いることで意味付けが容易なトピックを抽出できていることが確認できました．

考察

最終的に得られた事前分布のパラメータに注目してみます．

alpha :0.051928737413754714
beta :0.09577638564520818

もも0に近く，かなり小さな値になっていますね．

このパラメータに基づくディリクレ分布の振る舞いを可視化してみましょう． 可視化のコードはこれらの記事をパクりました．
多項分布とディリクレ分布のまとめと可視化 - ★データ解析備忘録★
Visualizing Dirichlet Distributions with Matplotlib
ありがとうございました．

まずはパラメータが(0.1, 0.1, 0.1)の3次元のディリクレ分布をプロットしてみましょう．

んー，一様ですか？よくわからないんで，パラメータを(0.99, 0.99, 0.99)にしてもう一度プロットしてみます．

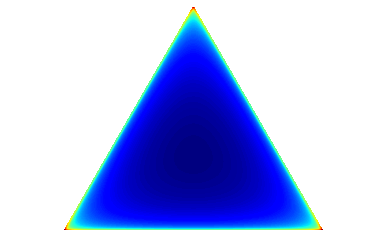
赤の方が値が大きく，青に近づくほど値は小さいです．
ということで，極端に偏った分布になっていたわけですね．

ここから生成されるベクトルのほとんどが，，，ということになります．

つまり，One-hotに近いベクトルが出現しやすい事前分布になっているわけですね．

事前分布は，"あっちのトピックとこっちのトピックがあり得そう"などという曖昧なものになりにくいことがわかりました．

おまけ

学習中はトピック1とトピック2の上位10単語をプリントさせました．
以下が学習の遷移です．

Epoch1

最初はほぼランダムなので一貫性はありません．

Epoch: 1
7343 / 7343
parameters
alpha :0.8956689597592044
beta :0.7423208433263517
---------------------
    topic1
こと    3802
年     3739
ため    2947
もの    2382
の     1848
場合    1502
数     1359
現在    1185
部     1009
万     1006
---------------------
    topic2
よう  4262
こと  2417
ため  2329
場合  2169
的   2078
部分  1382
これ  1270
もの  1251
関数  1208
漫画  1181
*********************

Epoch50

トピック2に数学系の単語が集まってきています． トピック1はこの段階ではよくわかりませんね・・・．

Epoch: 50
7343 / 7343
parameters
alpha :0.05620034268917989
beta :0.09405920652272919
---------------------
    topic1
こと    4213
もの    3076
よう    2191
ため    1969
日本    1850
的     1527
場合    1449
種     1225
の     1169
これ    1103
---------------------
    topic2
こと  6929
的   3302
数   3086
よう  2869
関数  2530
値   2311
定義  2197
集合  1975
空間  1954
単位  1905
*********************

Epoch150

トピック1にもなんとなく一貫性が出てきてます．
でもトピック1に名前つけるのムズイですねw
ダーウィンが来たとかですか？

Epoch: 150
7343 / 7343
parameters
alpha :0.051243695865978385
beta :0.09653944478736103
---------------------
    topic1
こと    2684
もの    1280
ため    1235
よう    1184
的     1153
年     1036
大陸    1030
動物     999
地球     958
種      942
---------------------
    topic2
こと  6211
数   2977
的   2833
関数  2493
よう  2456
値   2170
定義  2116
集合  1993
空間  1842
単位  1804
*********************

あとがき

本当はトピックモデルをユニグラムモデルから説明する記事を書こうとしてたんですが，途中で挫折してしまいました．

とにかく時間がかかりすぎる・・・．

一応下書きは保存してあるので，機会があれば書き切りたいです．多分書かないですがw

以上です．

1年間で読んだ本を振り返ってみる

お久しぶりです.

晴れて大学を卒業し, 4月から社会人になりました.

今は研修期間で割と時間がありますが, 本格的に仕事が始まっても, それを言い訳にせず記事を書き続けていきたいです.

さて1つの区切りとしていいタイミングなので, 何も考えず文系就職でいいやぁって感じだった僕が, データサイエンスに魅了され, この1年と3ヶ月の間で読んできた本を読んだ順にヒトコトつけつつ羅列してみます. 詳細なレビューはしません.

あともちろんですが, ここにあげた本の内容を完全に理解してるわけではないです. 全部読んでないものも多数あります. 今なら理解できるかもー！っていうのを思い出す作業って感じです.

目的 & ゴール

• 振り返りによって復習する部分を洗い出す.
• 学生と社会人でどの程度差が出るか, 来年知るための記録.

振り返り

1冊目: これならわかる最適化数学

手計算の例題が多かった. すごいいい本.

これなら分かる最適化数学―基礎原理から計算手法まで

2冊目: 数理最適化の実践ガイド

あんまり内容思い出せないから当時全然理解できてなかったぽい. 復習します.

数理最適化の実践ガイド (ＫＳ理工学専門書)

3冊目 深層学習

定番

深層学習 (機械学習プロフェッショナルシリーズ)

4冊目 コンピュータビジョン最先端ガイド

深層学習の章の図がめちゃくちゃわかりやすかったです.

コンピュータビジョン最先端ガイド6 (CVIMチュートリアルシリーズ)

5冊目 深層学習 Deep Learning

上の二冊で十分だった感ある.

深層学習 Deep Learning

6冊目 オンライン機械学習

Adamの説明とかあるし, 基本的なことも書いてあり初学者の僕には凄いよかった.

オンライン機械学習 (機械学習プロフェッショナルシリーズ)

7冊目 マセマ 統計学

この辺で, 統計検定の勉強を始めた. 多分5月くらい.
準1 & 2級は受かりました.

スバラシク実力がつくと評判の統計学キャンパス・ゼミ―大学の数学がこんなに分かる!単位なんて楽に取れる!

8冊目 統計学入門

マセマと同時進行させてた. 定番

統計学入門 (基礎統計学)

9冊目 マンガでわかる統計学 回帰分析編

めっちゃいい.

マンガでわかる統計学 回帰分析編

10冊目 マンガでわかる統計学 因子分析編

最高にわかりやすい.

マンガでわかる統計学 因子分析編

11冊目 多変量解析がわかる

これもかなりわかりやすかった.

多変量解析がわかる (ファーストブック)

12冊目 現場ですぐ使える時系列データ分析

実装なんもせずにざっと読んだままだ・・・.

現場ですぐ使える時系列データ分析 ~データサイエンティストのための基礎知識~

13冊目 統計検定２級 過去問

これで勉強は避けるべき.

日本統計学会公式認定 統計検定 2級 公式問題集[2014〜2016年]

14冊目 統計検定１級・準１級 過去問

1級は受けてないです.

日本統計学会公式認定 統計検定 1級・準1級 公式問題集[2014〜2015年]

15冊目 強化学習

将棋ソフトを作ろうと頑張りだした時期. アマゾンの評価ほど悪くないと思う.

強化学習

16冊目 コンピュータ囲碁

モンテカルロ木探索とか知りたくて買った.

コンピュータ囲碁 ―モンテカルロ法の理論と実践―

17冊目 Rで学ぶベイズ統計学入門

理論の説明は少なめ, ベイズ１冊目にしちゃだめな本だった. 三章までしか読んでないや.

Rで学ぶベイズ統計学入門

18冊目 ベイズ統計学入門

めちゃめちゃいい本だった. でも7章から闇深い.

ベイズ統計学入門

19冊目 PRML 上巻

式番号で検索すれば解説がヒットする. むずい. 下巻は眠ってる.

パターン認識と機械学習 上

20冊目 劣モジュラ

未知の領域だった. 使えるかもしれない！って業務に出会ったらまた戻ってきたい.

劣モジュラ最適化と機械学習 (機械学習プロフェッショナルシリーズ)

IPython クックブック

辞書的使い方

IPythonデータサイエンスクックブック ―対話型コンピューティングと可視化のためのレシピ集

Numpy, Pandas

同じく, 辞書的使い方

Pythonによるデータ分析入門 ―NumPy、pandasを使ったデータ処理

まとめ

休憩がてら適当に書いた記事で, 誰のためにもなっていないような気がしますが気にしません.

今年度は何冊程度読めるのか・・・. 数だけじゃなくて質も上げていかないとって感じですね. 頑張ります.

以上です.

RustでForward自動微分を実装してみた

Rustの理解がまだまだすぎて. モジュールとして全く使えない実装になっているので悪しからず. Forward自動微分そのものを理解することを目標とします.

ちなみに僕が参考にしたのは以下のサイトです.

• 自動微分 - Wikipedia
• ボトムアップ型自動微分の実験 - kivantium活動日記
• 自動微分を実装してみた - Nosの日記

ありがとうございました.

自動微分とは

自動微分そのものの説明は上にあげたサイトがとても詳しく説明しています. 数値微分を理解している人ならば, 簡単に違いを理解できると思います.

自分なりに自動微分を簡単にまとめると,
導関数を先に定義して計算効率&精度を上げようって感じです.
例えば, の微分はである, と先に定義しておくわけですね.

参考にしたサイトと同じようなことを説明しても意味はないと思うので, ここでは例を複数あげることで理解の助けになれればと思います.

とりあえず, Forward自動微分の実装で重要なのは, 以下の3点だと自分は理解しました.

• 二重数と呼ばれる, Dual型の定義
• Dual型に対する基本演算の定義
• Dual型の初期値の設定

1つずつ詳しく見ていくことで, どの言語でも実装できるような説明を心がけてみます.

Dual型の定義

Dual型はある変数とその微小量を表すをもつ型です.
Rustでは以下のように実装しています.

#[derive(Debug, Copy, Clone)]
pub struct Dual {
    var: f32,
    eps: f32,
}

みてわかる通り, 普通の変数に微小量がくっついただけなので, int型やfloat型の拡張と考えていいと思います.

基本演算の定義

では, 次にDual型に対する基本演算を定義します.
というより, 微小量に関する基本演算を定義します.

例として, まずは和を定義してみましょう.

こんな式があったとします.

突然ですが, このをに関して微分して見てください.

・・・はい. 恐らくみなさんの頭の中では第1項, 第2項をそれぞれ微分して最後に和をとる, というような暗算をしただろうと思います.

より詳しくいうのであれば, まず第1項を計算する.

次に第2項も微分する.

そして最後に和をとる.

以上のようなステップを踏むことで, のに関する微分を導いたと思います.

ここで重要なのは最後に和をとったことです.

つまりの微小量は, それぞれの項の微小量を単に足すことで求めることができます.

より簡潔に言うならば, 和の微分は微分の和ということです.

以上のルールに則りRustでDual型の和を定義するとこのようになります.

// + 演算子のオーバーロード
impl Add for Dual {
    type Output = Dual;
    fn add(self, r: Dual) -> Dual {
        Dual {
            var: self.var + r.var,
            //ある変数の和に対する微小量の和を定義する.
            eps: self.eps + r.eps
        }
    }
}

それでは次に積を定義をしてみましょう.
先ほどと同じように具体例を出してみます.

和の時と同様にで微分してみてください.

・・・はい. 今度は高校の時に呪文のように覚えた微分そのまま, そのまま微分のルールに基づいて暗算したのではないでしょうか. (この呪文は僕だけかもしれませんが…)

具体的に書いてみると,

こうですね. それではこのルールに則りDual型の積, もといDual型の微小量に対する積を定義しましょう.

//　積のオーバーロード
impl Mul for Dual {
    type Output = Dual;
    fn mul(self, r: Dual) -> Dual {
        Dual {
            var: self.var * r.var,
            // ある変数の積に対する微小量の積を定義する.
            eps: self.eps*r.var + self.var*r.eps
        }
    }
}

以上のように差や商に関してもDual型の演算を定義してあげることで, 勝手に微小量が計算されちゃうよっていう寸法です.

ここで簡単な式に実践してみましょう.

この式の微分は

ですね. 簡単です. この式によるとの点での傾きは5です. さてDual型を使ってこの5は計算できるのか.

// 式の定義
fn example1(x: Dual) -> Dual {
    x*x + x
}

fn main(){
    // x = 2　なので varは 2 とします.
    let x = Dual{var: 2f32, eps: 1f32};

    println!("{:?}", example1(x));
}

出力

Dual { var: 6, eps: 5 }

おーちゃんと計算できてますね！

先ほど説明した四則演算のように, やも定義してあげればこれらの演算が入っている式でも問題なく傾きを求めることができます.

こんな感じでざっと定義してあげて…

impl Dual {
    fn sin(self) -> Dual {
        Dual {
            var: self.var.sin(),
            eps: self.eps*self.var.cos()
        }
    }

    fn exp(self) -> Dual {
        Dual {
            var: self.var.exp(),
            eps: self.eps*self.var.exp()
        }
    }
}

こいつらを含んだ式を適当に作ってあげて…

fn example2(x: Dual) -> Dual {
    x.sin() + x*x.exp()
}

の傾きを求める！

fn main(){
    // x = 0
    let x = Dual{var: 0f32, eps: 1f32};
    
    println!("{:?}", example2(x));
}

出力じゃ！！

Dual { var: 0, eps: 2 }

おもしれェェェエエエ！

仕組みは単純なのに簡単に傾きが求められる！やばい！

初期値の設定

ここでより一般的な拡張を考えてみると,

おいおい, 多変数関数の時はどうすんだい？

ってなりますよね. 実はForward modeは多変数関数に弱いんです. でもDual型の初期値の設定によって一応求めることができます.

例えばこんな式を用意しましょう.

そしてのによる偏微分を求めてみる. 手計算するとこうです.

に関する傾きを求めるには次のように初期値を設定してあげましょう.

let x = Dual{var: 0f32, eps: 1f32};
let y = Dual{var: 2f32, eps: 0f32}; // epsを0にする！

つまりのに対する微小量はと, 定義してあげます.　上のように定義すると出力は

Dual { var: 2.9092975, eps: 4 }

こうなります. 実際,

なのであってますね！逆にの偏微分を求めるには,

let x = Dual{var: 0f32, eps: 0f32}; // epsを0にする！
let y = Dual{var: 2f32, eps: 1f32}; 

こうすればOKですね.

1度の演算で1つの変数に対する傾きしか求められないのが残念ですね.

全ての変数に対して1度の演算で勾配を求められるのがBackward modeなのですが, ちょっとまだ理解できてません. と言うか仕組みはわかるけど実装ができない・・・. もうちょっと勉強してみます.

一応全コード載せとく

use std::ops::{Add, Sub, Mul, Div};
use std::f32;

#[derive(Debug, Copy, Clone)]
struct Dual {
    var: f32,
    eps: f32,
}

// + 演算子のオーバーロード
impl Add for Dual {
    type Output = Dual;
    fn add(self, r: Dual) -> Dual {
        Dual {
            var: self.var + r.var,
            //ある変数の和に対する微小量の和を定義する.
            eps: self.eps + r.eps
        }
    }
}

impl Sub for Dual {
    type Output = Dual;
    fn sub(self, r: Dual) -> Dual {
        Dual {
            var: self.var - r.var,
            eps: self.eps - r.eps
        }
    }
}

//　積のオーバーロード
impl Mul for Dual {
    type Output = Dual;
    fn mul(self, r: Dual) -> Dual {
        Dual {
            var: self.var * r.var,
            // ある変数の積に対する微小量の積を定義する.
            eps: self.eps*r.var + self.var*r.eps
        }
    }
}

impl Div for Dual {
    type Output = Dual;
    fn div(self, r: Dual) -> Dual {
        Dual {
            var: self.var / r.var,
            eps: self.eps/r.var - r.eps*self.var/r.var/r.var
        }
    }
}

impl Dual {
    fn sin(self) -> Dual {
        Dual {
            var: self.var.sin(),
            eps: self.eps*self.var.cos()
        }
    }

    fn cos(self) -> Dual {
        Dual {
            var: self.var.cos(),
            eps: -self.eps*self.var.sin()
        }
    }

    fn tan(self) -> Dual {
        Dual {
            var: self.var.tan(),
            eps: self.eps/(self.var.cos()*self.var.cos())
        }
    }

    fn exp(self) -> Dual {
        Dual {
            var: self.var.exp(),
            eps: self.eps*self.var.exp()
        }
    }
}

fn newton_sqrt(var: Dual) -> Dual {
    let mut y = Dual{var:2f32, eps:0f32};
    let two = Dual{var:2f32, eps:0f32};
    for i in 0..10 {
        y = (y + var/y) / two;
        println!("{:?}", y);
    }
    y
}

// 式の定義
fn example1(x: Dual) -> Dual {
    x*x + x
}

fn example2(x: Dual) -> Dual {
    x.sin() + x*x.exp()
}

fn example3(x: Dual, y: Dual) -> Dual {
    y.sin() + x*y + y*x.exp()
}

fn main(){
    // x = 0 の傾きを求めてみる
    let x = Dual{var: 0f32, eps: 1f32};
    let y = Dual{var: 2f32, eps: 0f32};

    //println!("{:?}", example2(x));
    println!("{:?}", example3(x, y));
    //println!("{:?}", newton_sqrt(var));
}

まとめ

1年前に僕の尊敬する師匠から自動微分の話を聞いたのですが, 当時は全く意味がわかりませんでした. そもそもコンピュータがどのように微分しているかすら考えたことなかったですからね.

Backward modeも頑張って実装したいところ・・・.

以上です.